Leetcode 第4题 - 寻找两个正序数组的中位数(hard)
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3] nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2] nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
解题思路
最简单的方法 就是先合并 ,然后找到 中位数取出。
这里的知识点是小学数学我们学过的 取一组数的中位数,如果是 奇数个 假设数组长度 为 m ,那么 就是 ceil(m / 2) ceil 是向上取整 比如 arr[ceil(9/2)] = arr[5] ,如果是偶数 那么 就是 取第ceil(m/2) 和 第ceil(m /2 + 1) 相加
比如 arr[ ceil(10 /2 )] +arr[(ceil(10 /2) + 1)] =arr[5] + arr[6] 。
那么 我们需要做的 就是 把2个组数 在合并后每个数对应合并后的索引给找出来,这样 通过计算出来的 中位数的索引就可以确定 中位数了。
双指针归并
时间复杂度:O (m+ n)
空间复杂度:O (1)
中位数的计算,如果数组是 奇数个 直接取 中间的数 [ 1,2 ,3] -> 2
如果数组是偶数个 取中间的 2个数相加除以 2 [1,2,3,4] -> 2 + 3 / 2 =1.5
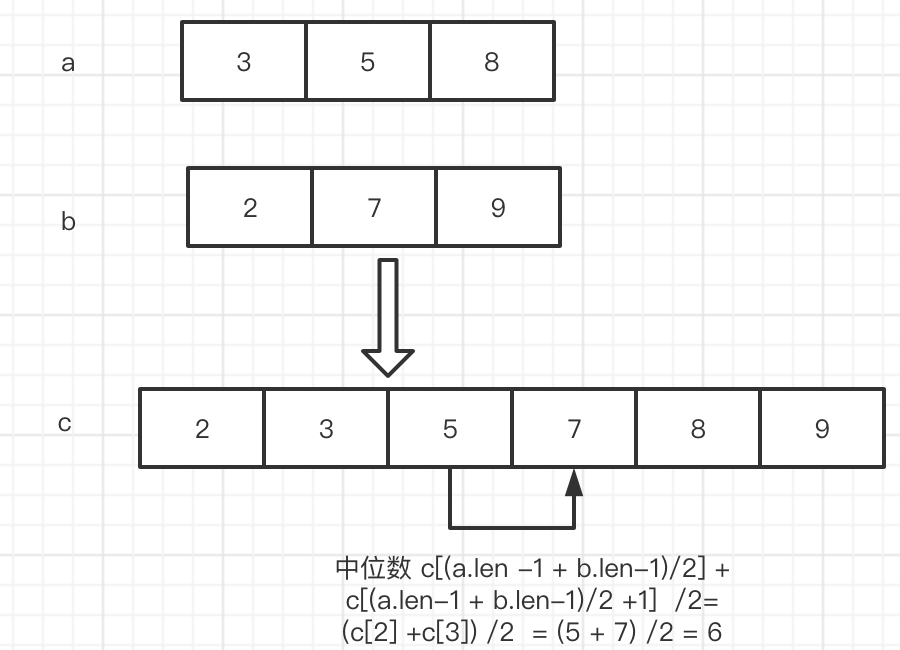
那么 由于数组原先就是有序的,我们 可以使用归并 定义2根指针 然后依次 比大小,然后不停的往后取。
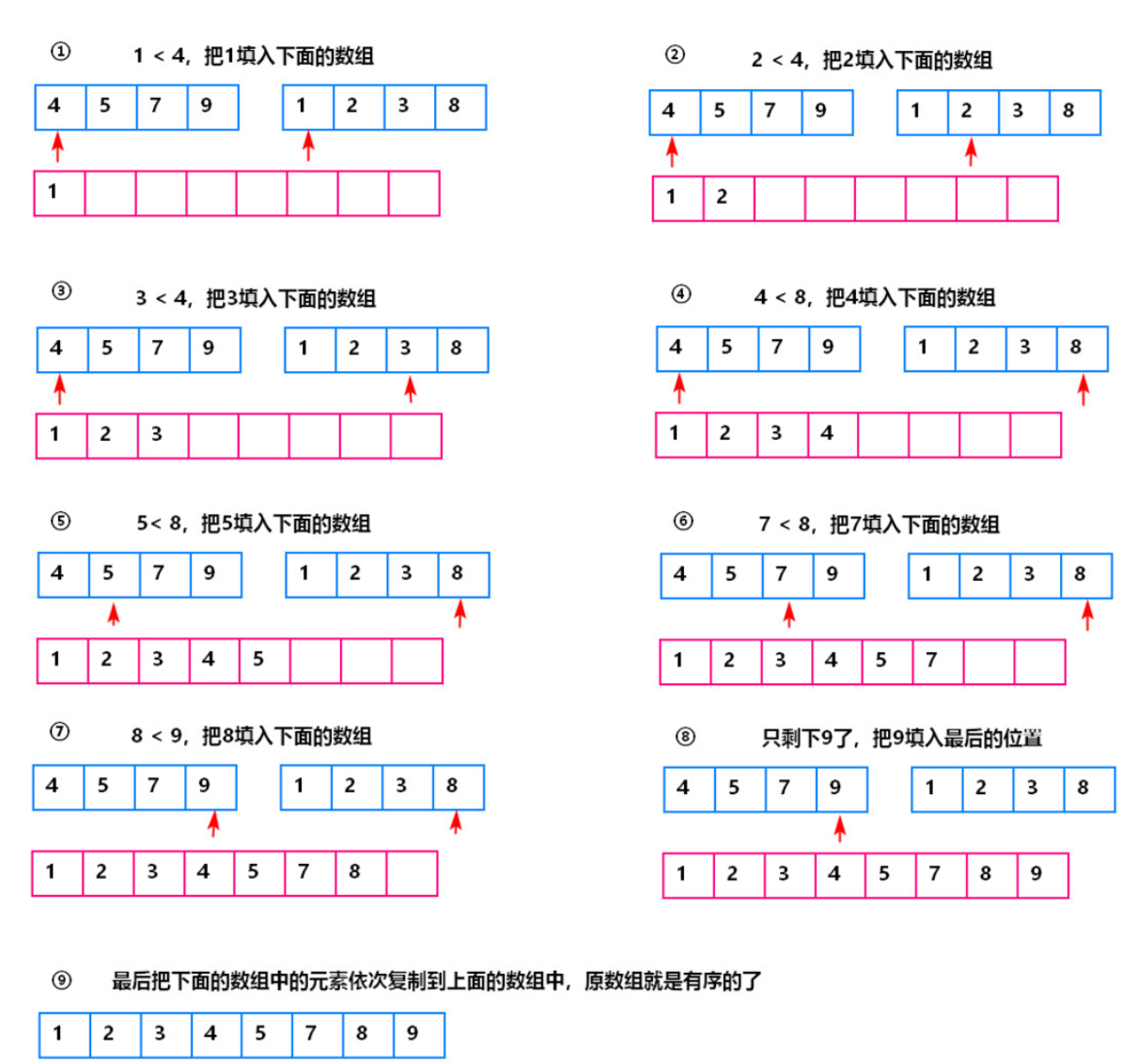
pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64 { let mut pointer_a = 0; let mut pointer_b = 0; loop { // 这个判断取的是公共长度的 部分 a 如果 长度为 5 b如果长度为 4 那么 这个判断里面 是 前 4个数归并 if pointer_a > nums1.len() || pointer_b > nums2.len() { if nums1[pointer_a] < nums2[pointer_b] { //如果 指针a的值 < 指针b的值 指针 a 往后移动一个位置 println!("{}",nums1[pointer_a]); pointer_a +=1; }else if nums1[pointer_a] > nums2[pointer_b]{ //如果 指针a的值 > 指针b的值 指针 b 往后移动一个位置 println!("{}",nums2[pointer_b]); pointer_b +=1; }else if nums1[pointer_a] == nums2[pointer_b]{//如果两个数 相等 2根指针 都往后移动1个位置 println!("{}",nums1[pointer_b]); pointer_a +=1; pointer_b +=1; } }else if pointer_a < nums1.len(){ //当 b指针的 长度 耗尽 了 我们只需要移动 a 指针就好了 println!("{}",nums1[pointer_a]); pointer_a +=1; }else if pointer_b < nums2.len(){ // 当 a指针的 长度耗尽了 ,接下来 我们只需要移动b 指针了 println!("{}",nums2[pointer_b]); pointer_b +=1; }else{ //上述条件都不满足,跳出循环 break; } } 1 as f64 } fn main() { let mut a1 =vec![1,3,5,12,16]; let mut a2 =vec![2,4,6,7,9]; find_median_sorted_arrays(a1,a2); }
上面的 代码 我们久通过指针 指向了 2个数组,然后比较大小 然后移动指针,代码 比较简单 就是 定义 双指针 比大小 然后 移动指针。 要注意的是 由于2个数组长度不一样,当一个数组长度到头了,那么就移动剩下的数组指针到结束为止。
上面其实就实现了 将 2个有序数组进行归并的过程,实际上我们 没有定义一个数组 来存放 归并好的值,因为不需要这么做 我们直接通过 2根指针的 位置相加 计算出 每个数在 归并后数组的索引,如果 等于2个数组合并后中位数的索引 那么就找到了这个值。
但我们在编码的过程中,我们计算中位数索引的值需要注意,一点:
- 我们对给定的2个数组长度相加是奇数和 偶数 做一下判断,如果是奇数 直接取 最中间的一个数,如果是 偶数要取到 中间的 2个数相加 再 除以 2。
pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64 { // 这个判断 是为了 处理一些 比如 [] ,[1] 这样糟糕的数据,偷懒 就直接在这处理掉吧! if (nums1.len() ==1 && nums2.len() == 0) { return nums1[0] as f64; } if(nums1.len() ==0 && nums2.len() == 1) { return nums2[0] as f64; } let mut pointer_a = 0; let mut pointer_b = 0; //flag 用于记录最后一次移动的 是 pointer_a 或者 是 pointer_b 或者都移动了 let mut flag = 0; let mut lastnum =0; loop { // 这个判断取的是公共长度的 部分 a 如果 长度为 5 b如果长度为 4 那么 这个判断里面 是 前 4个数归并 if pointer_a < nums1.len() && pointer_b < nums2.len() { if nums1[pointer_a] < nums2[pointer_b] { //如果 指针a的值 < 指针b的值 指针 a 往后移动一个位置 flag = 0; }else if nums1[pointer_a] > nums2[pointer_b]{ //如果 指针a的值 > 指针b的值 指针 b 往后移动一个位 flag = 1; }else if nums1[pointer_a] == nums2[pointer_b]{//如果两个数 相等 2根指针 都往后移动1个位置 flag = 2; } }else if pointer_a < nums1.len(){ //当 b指针的 长度 耗尽 了 我们只需要移动 a 指针就好了 flag = 0; }else if pointer_b < nums2.len(){ // 当 a指针的 长度耗尽了 ,接下来 我们只需要移动b 指针了 flag = 1; }else{ //上述条件都不满足,跳出循环 break; } //上面的所有代码 主要负责 循环移动a b 的指针,直到数组的末尾,需要 注意的 是 数组 总是有长有短 如果一边的指针 移动到末尾了 剩下的 全部移动 另一边的指针 //如果 指针 指向了 中位数 if ((nums1.len() + nums2.len() -2 ) / 2) + 1 == pointer_a + pointer_b { //如果 数组1 + 数组2 是奇数个 if (nums1.len() + nums2.len()) % 2 != 0 { //处理 指针 a 移动了的情况 if flag == 0{ return nums1[pointer_a] as f64; }else { //如果指针 b 或者 2个指针都移动 的 情况 return nums2[pointer_b] as f64; } }else{//如果 数组1 + 数组2 偶数个 //如果 是 偶数个 我们 需要 记录上一个数 和当前的 数相加 / 2 if flag == 0{ return (nums1[pointer_a] as f64 + lastnum as f64) / 2.00; }else { return (nums2[pointer_b] as f64 + lastnum as f64) / 2.00; } } //处理 pointer_a 和 【pointer_b 相等 都往后 移动 2步,那么 pointer_a + pointer_b == 数组1长度 + 数组2长度 -2 (从0索引开始 所以 -1 -1 = -2) /2 + 1 }else if (nums1.len() + nums2.len() -2 ) / 2 + 1 < pointer_a + pointer_b { break; }else{ //如果 不是中位数 if flag ==0{ lastnum = nums1[pointer_a]; //指针 a 往后移动一步 pointer_a += 1; }else if flag ==1{ lastnum = nums2[pointer_b]; //指针 b 往后移动一步 pointer_b += 1; }else{ lastnum = nums1[pointer_a]; //指针 a b 分别往后移动一步 pointer_a += 1; pointer_b += 1; } } } return lastnum as f64; } fn main() { let mut a1 =vec![1,2]; let mut a2 =vec![3,4]; println!("{}",find_median_sorted_arrays(a1,a2)); }
第一次 执行用了 8ms,后面执行 就变成 4ms了,不知道什么原因。
二分法
在 上面一种方法中,我们定义了 2根指针 从头开始 取计算 中位数对应的数,但实际上 我们可以 直接 用 二分法 每次折半 来缩减 查找的 范围。
假设 给定 2个数组 ,长度 分别为 6 和 5.
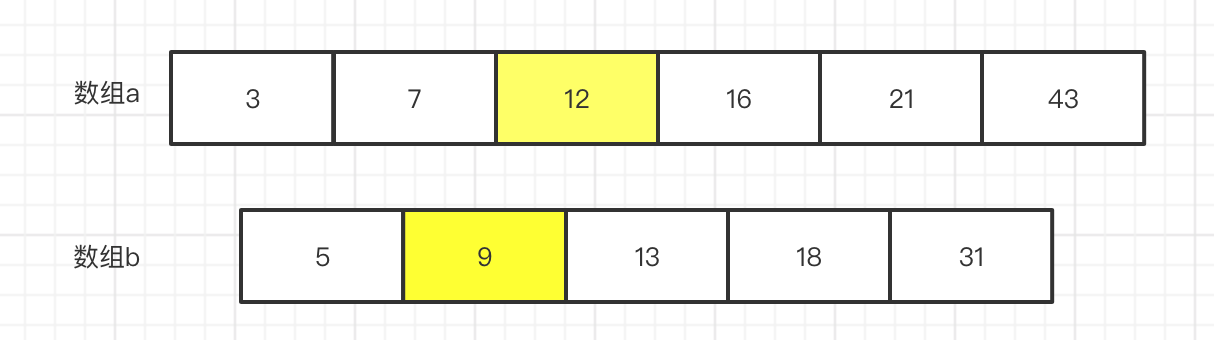
让我们 思考一个问题,什么是中位数,假定 我们 在 数组a 和数组b 中找到一个中位数,那么 不考虑 偶数个 中位数 就是 前边 和 后边的长度是一样的。
假设 数组 a 的长度为 m,数组b的长度 为 n
那么 中位数的位置 就是 (m + n + 1) / 2, 那么 意思是 我们只需要找到 一个数,它前面有 (m + n + 1) / 2 -1 个数那么 它不就
是中位数了吗。
如上图,如果我们假设 7 是中位数,那么 怎么石锤 这个证明呢?
只要证明 小于等于 7的 数是否有 (m + n + 1) / 2 -1 个不就好了吗 ?
那问题进一步的 变成 怎么 计算 <=7 的数的个数呢?
那么 首先 数组 a 中 7的索引是 1 那么 我们就说 数组a 中小于等于7的 有一个数,在数组a中找比起小的很容易.
那么 问题又变成了 怎么在 数组b 中找 <=7 的数的个数呢?
那么 逐个搜索不就好了吗,但是 有没有更好的方法呢? 既然给定的 数组b 是有序的那我们 就可以考虑 使用更高效的 搜索方法,对于有序的数组 抖索效率 最高的当然是属 二分搜索啦。
那么 我们可以肉眼看到 数组 b 中,<=7 的只有 1个 那么 加上 数组a 中的 一个 总共 就是 2个数, 12 / 2 -1 = 5 很明显,不符合 。
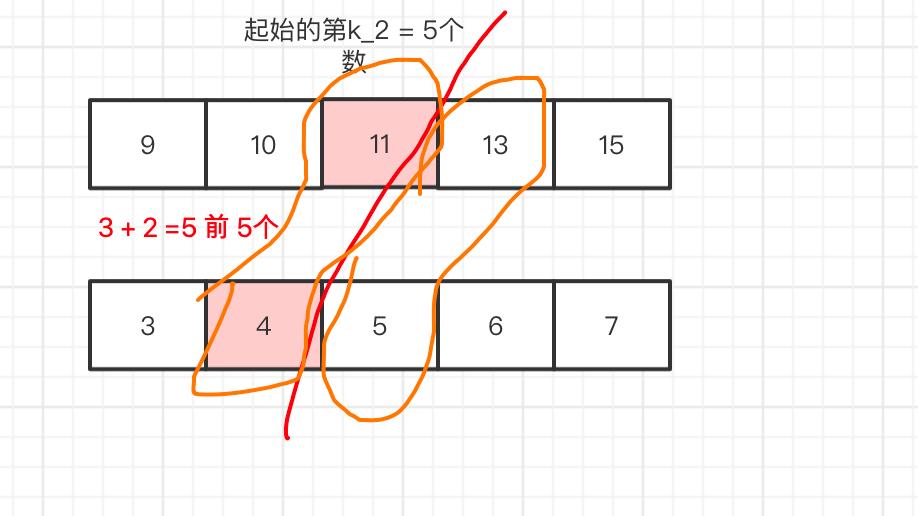
那么 我们使上帝视角 稍微观察下 就知道 中位数是13 是中位数,
那么 我们还是 证明下吧 13 的 index = 2, 数组 a 中 <= 13 的数 有 3 个,那么 3 + 2 = 5, 前面正好有 (m + n + 1) / 2 -1
个 数那么 它的确是中位数。
总结
根据上面的 证明 我们可以得出:
我们 可以先随机定义一根指针a,指向某个数,然后在另一个数组也定义一根指针b,
然后 我们假设 指针a 为 中位数 然后去指针 b 找 小于等于 a指针的个数,使用二分查找,每次 筛选掉一半,
然后再判定下 指针 a 是否有前 (m + n + 1) / 2 -1 个数 。
如果 a 前面的数 > (m + n + 1) / 2 -1 说明 我们 要把 a 指针 往前 移动
如果 a 前面的数 < (m + n + 1) / 2 -1 说明 我们 要把 a 指针 往后 移动
a指针 我们也每次移动 剩余范围的一半,采取这样的二分法。
这里我们 还要注意 如果 a 数组 里面找不到中位数,那么 我们就需要 直接在 b数组里面找中位数。
另外要注意的是 我们 希望是 在数组 a 里面找到 中位数,那么 要求 数组a的长度 >= 数组b 的长度,所以我们 在一开始判断下谁的长度长 就是数组a 最下数组交换。
用这种方法,要处理很多 边界条件,太烦了 写了 70% 放弃。
找第 k 个数
条件 给定数组 a 长度为 m,数组b 长度 为 n
那么 数组 a 和数组 b 的中位数 为 (m + n + 1) / 2 为什么 + 1 呢? 主要是向上取整floor。如果不加 1 那么就是向下取整。 Floor(1.x) =2 , ceil(1.x) = 1。
二分法介绍
如果给定一个 从小到大的数组,那么怎么快速查找一个数,一般使用二分法。二分法 是不断缩小搜索范围的一种方法。
第一次 搜索范围一半 (m + n + 1) / 2 一半分为 左边一半 和 右边一半
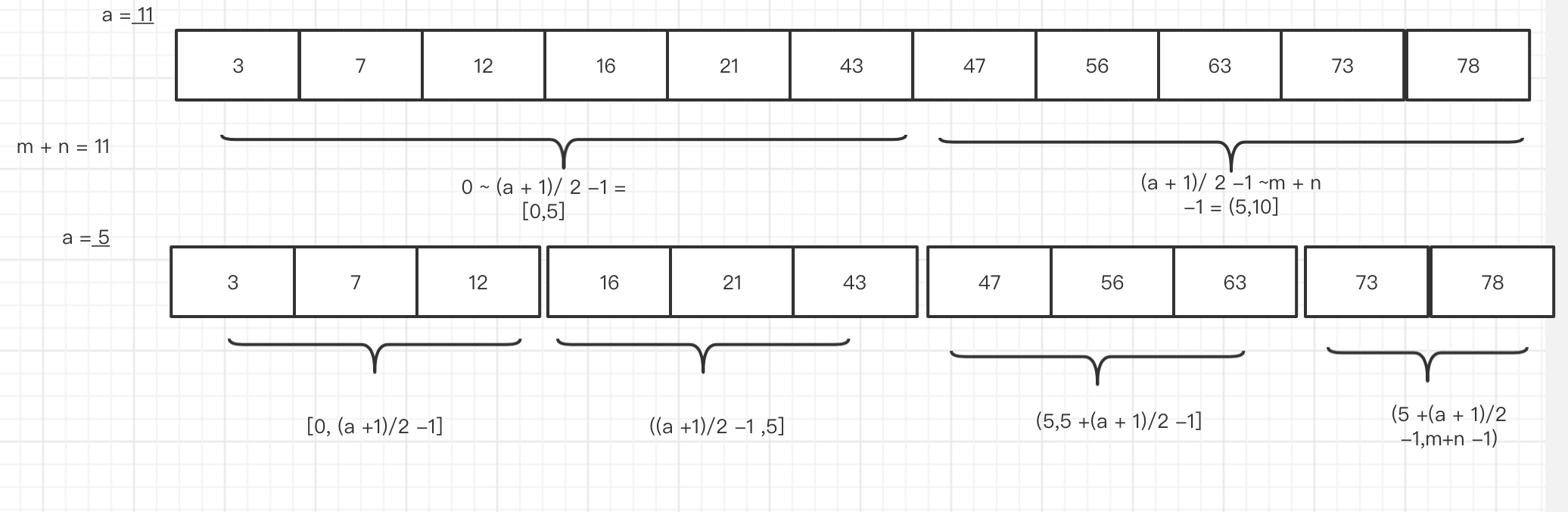
二分法 是 每次都除以 2 这样 然后 收敛在 0点, 5 -> 2 -> 1 -> 0。
我们 如果从给定的数组m 中去取第k个数,那么 它的前 面的 k -1 个数必然是小于等于 第k个数的。
那么 我们如果在 第二数组也找到第 k_ 个数,也是同样的结果,那么当我们 把第 数组 a 的 第k 个数和数组 b 的第k个数作比较,那么 必然有一方 大于或等于 另一方, 假设 数组 a 的 k为k_1 数组b 的 k为 k_2,假设 k_1 >= k_2,那么 我们可以得出 2k -1 个数 不等于 第 2k 个数.
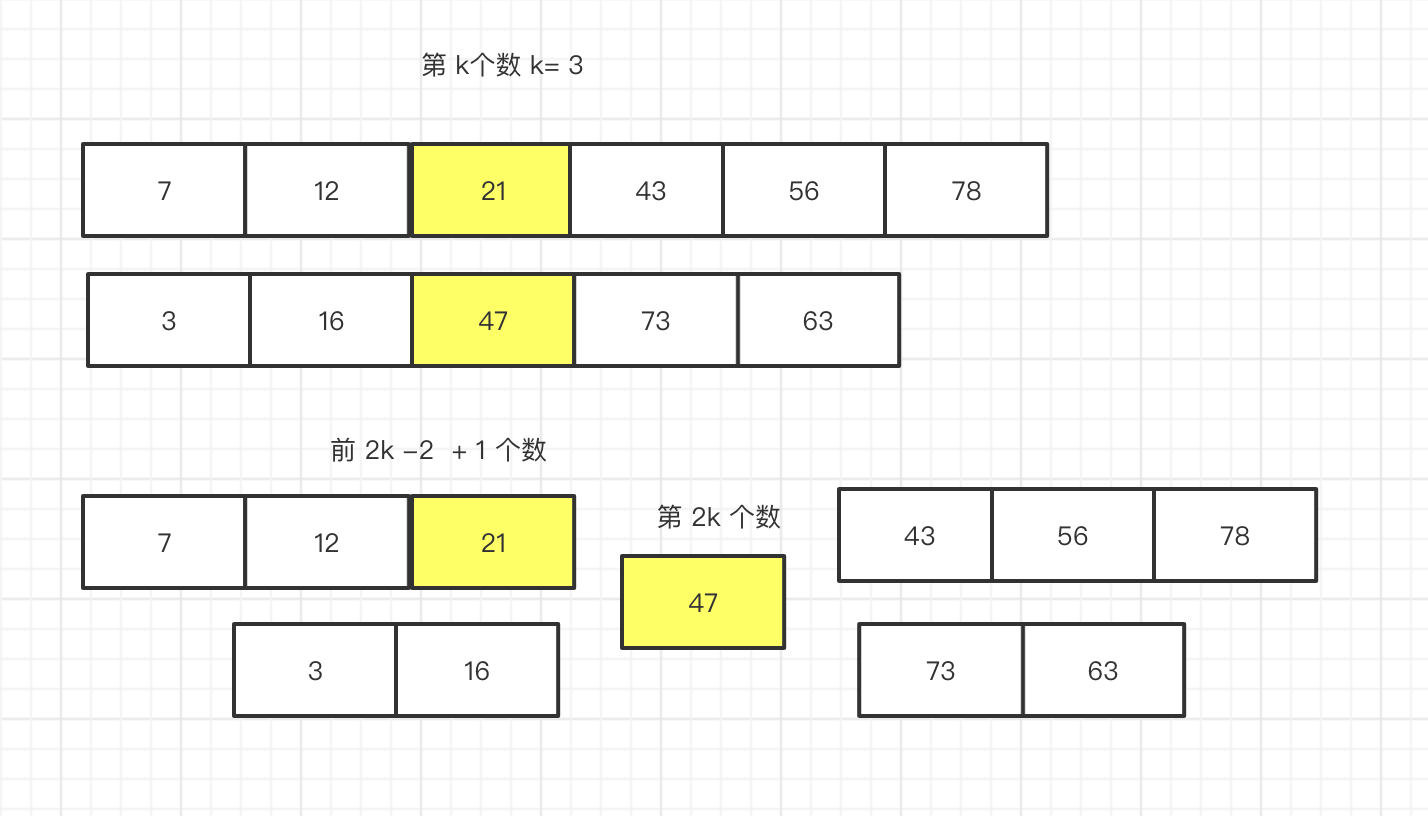
那么 就排除前 2k -1 个数 了, 如果 k_1 要想成为 第 2k 个数,要满足 条件 k_2 的 第 k_2 + 1个数 > 第 k_1个数,
否则的话 第 k 个数。如上图 假设 47 为 第 2k个数,他前面有 2k -1个数比它小。
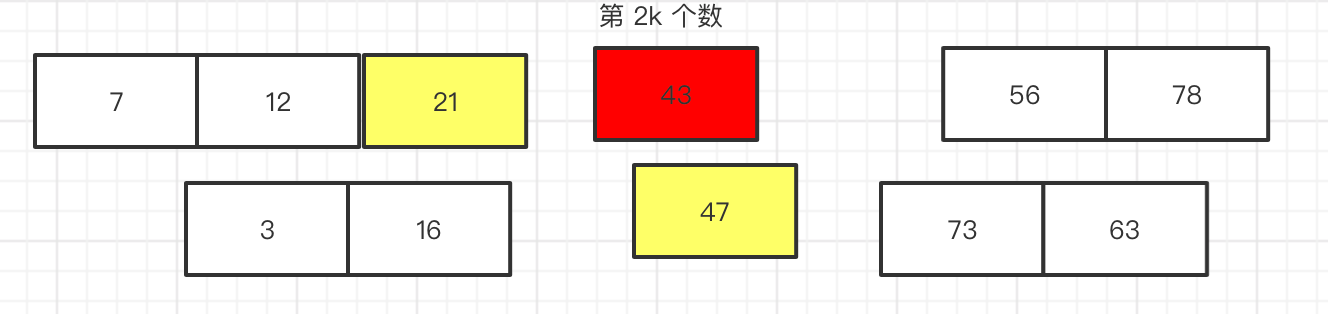
如上图 我们可以看到,当数组 b 中 第 k + 1 个数 比 47 小了 那么 k就会变成 第 k + 1 个了,就好像 有人问你 跑过了 倒数第二名 你是第几名一样, 由于 43 比 47小所以 就替换了 47的位置 此时 43 变成了 第 k 位数。
代码实战
光说不练假把式,我们 可以用上面的思维 边完成代码 边继续推理,能边学习边及时得到反馈 也能让你更有兴趣对问题更加深入的研究。
1. 首先 我们 要定义 2k 是多少, 我们 一般 把 2k 取为 中位数 的位置?
假设 2个数组 m 长为 3 n长为 2 ,按照中位数的计算 应该取 (3 + 2 + 1) / 2 = 3
那么 我们可以在 m 里 取 2,那在 n里取到 3 -2 = 1(注意实际索引 从 0开始 要 -1 但是为了方便了解这里 使用从1开始)
但是 如果 m 是个只有为 1的数组 那怎么办呢? 所以 我们在 取值的时候可以采用 将中位数 3/2 = 1 然后我们再判断下,如果 数组索引 比 1大 k_m取 1 比1小 k_m 取数组的长度。
然后k_n + k_m =3 , k_n取剩下部分。
pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64{ let mut nums1 = nums1; let mut nums2 = nums2; if nums1.len() > nums2.len(){ let tmp = nums1; nums1 = nums2; nums2 = tmp; } let k_2 = (nums1.len() + nums2.len() + 1) / 2 -1; //k 为小的数 let mut k_m = nums1.len() -1; let mut k_n = 0; let k = k_2 / 2 ; if k_m < k{ k_n = k_2 - k_m -1; }else{ k_m = k; k_n = k_2 - k -1 ; } println!("{},{}",pointer_a +1,pointer_b +1); } fn main() { let m = vec![7,12,21,43,56,78]; let n = vec![3,16,47,73,63]; find_median_sorted_arrays(m,n); }
上面代码 k_2 变量名 就是 2k 个数的索引 也就是中位数索引,由于变量起名规则,下文 我们一致 用第K_2 个数 来替代 第2k 个数
2.如何找到中位数?
有了上面的划分 我们 就要来证明,如何找到中位数的位置呢.
我们知道 数组是从大到小有序的,并且上面的算法 把数组 划分成了这样
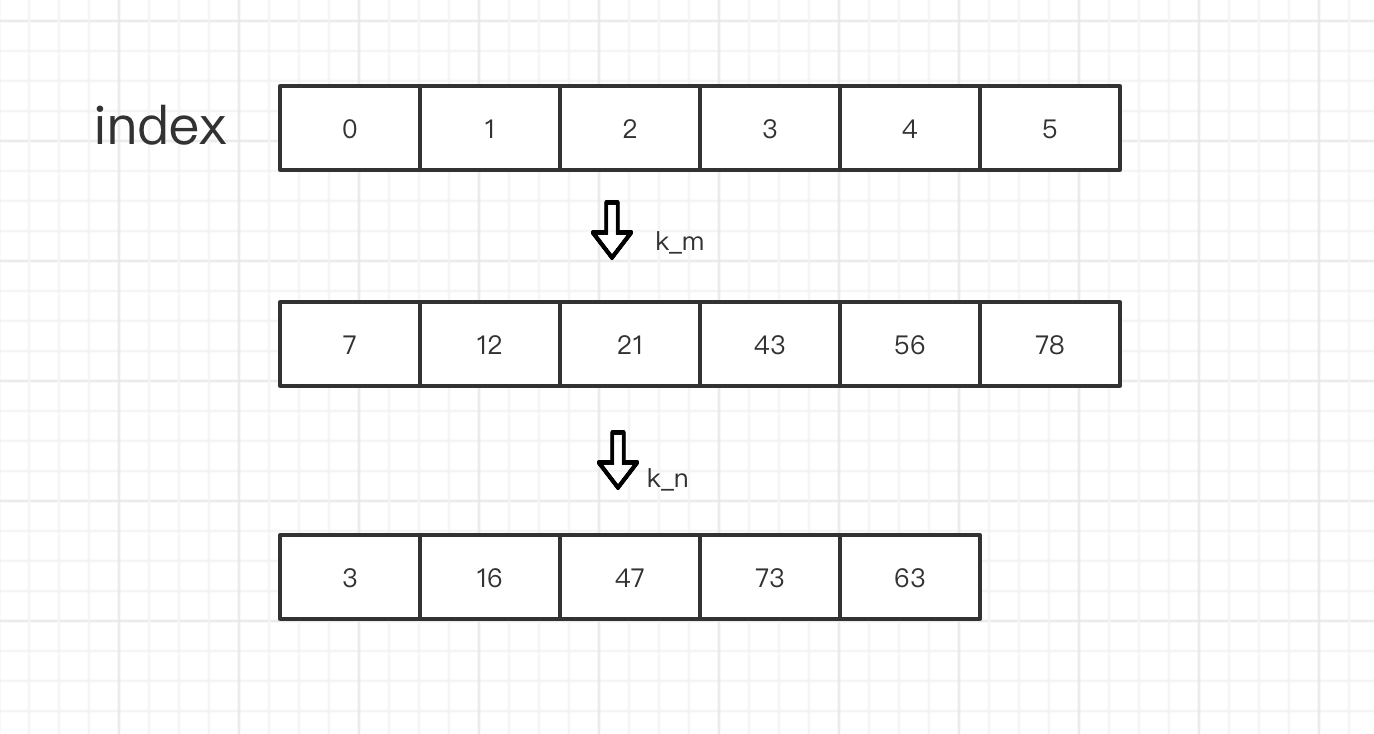
那么 我们首先尝试去 比较 k_m 和 k_n 的大小 谁大 我就认为 设就是暂时的第k_2个数,
#![allow(unused_variables)] fn main() { //谁大 谁就是 k_2 个数 if nums1[pointer_a] > nums2[pointer_b]{ println!("{} ",nums1[pointer_a]); }else{ println!("{} ",nums2[pointer_b]); } }
那么 有了k_2 个数,我们 就要到中位数了吗? 其实还有挺长的路要走。
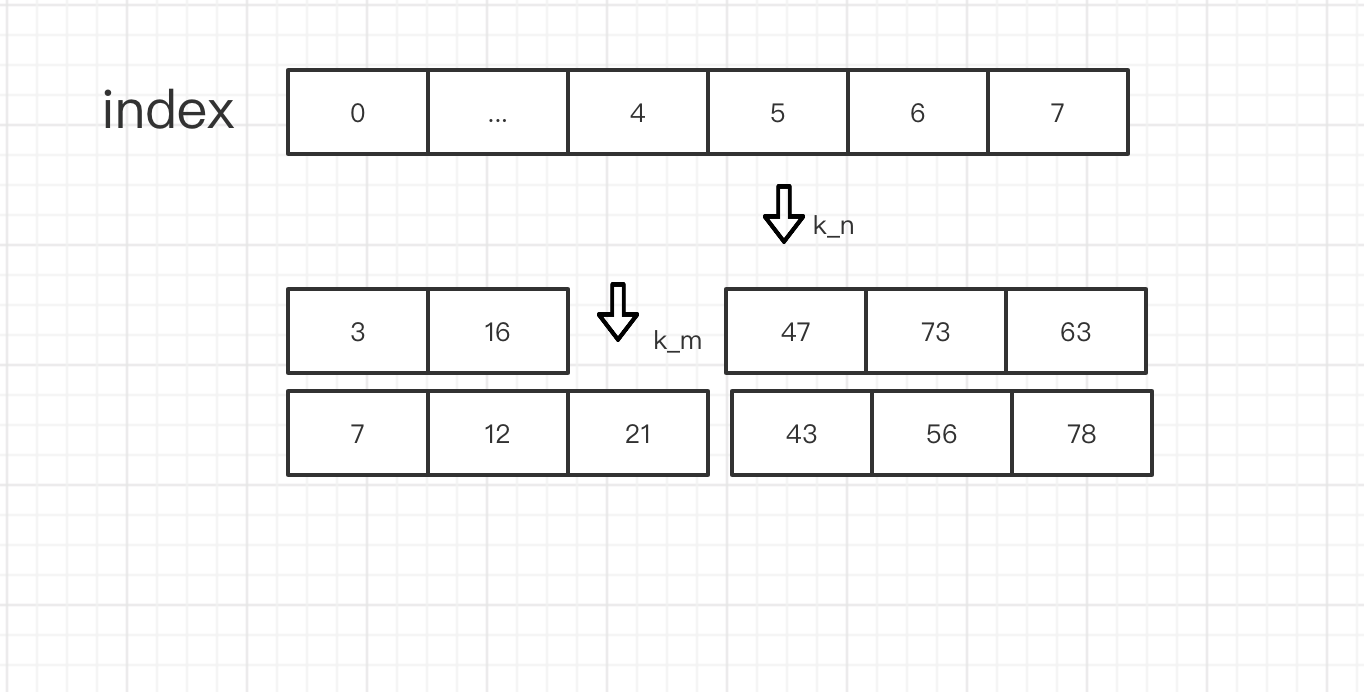
现在 呢 47是 第 k_2个数,但是 因为它前面有 k_2 - 1个数,那么想要维持住这种关系,那么 我们就要保证
k_m 和 k_n 后面的数全部 要 大于 47, 由于 已知 是给定数组是升序排列的,就有 k_n + 1 > k_n
那么 k_m 后面的数,就决定这 k_n 是不是 第 k_2 个数的关键。
此时 就会有两种情况:
- k_m + 1 < k_n 如果是 这种情况,那么 k_m + 1 将会插到 k_n 前面,使得 k_n 变成第 k_2 + 1 个数,而 k_m + 1变 成 第 k_2 个数。又 由于 k_m + 1 < k_m + 2 那么,k_m + 1 前面不可能再插入其他数了,所以k_m + 1 就变成了k_2。 当然 在实际编码过程中,我们还要注意 k_m + 1 是否存在。
- k_m + 1 >= k_n 这种情况,k_m + 1 不能插入到k_n 前面所以不会影响 k_n ,所以不需要做什么.
那么 分别讨论了上面2中问题,是不是就能 覆盖了所有问题了呢?
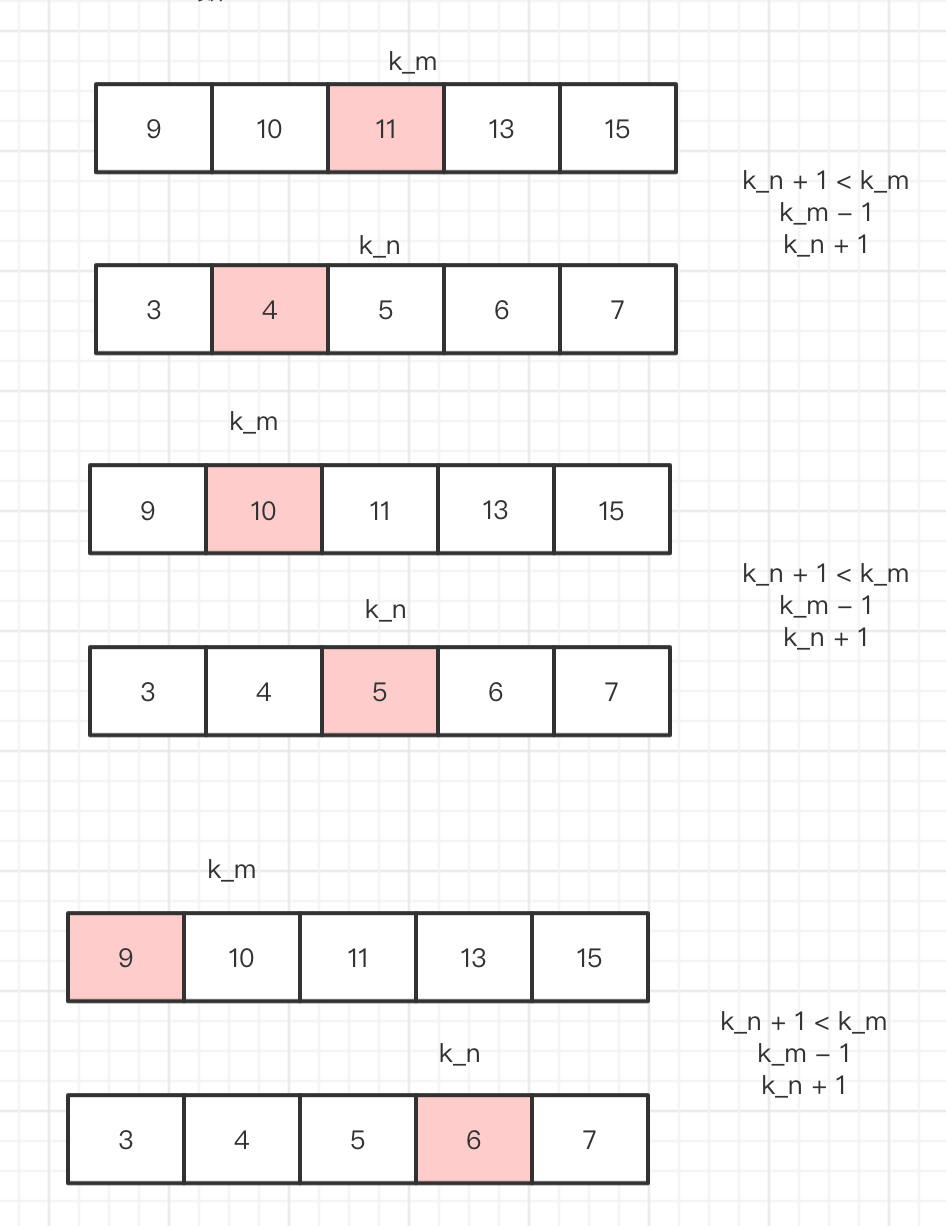
第一种情况 我们 还需要小心一点,如下图:
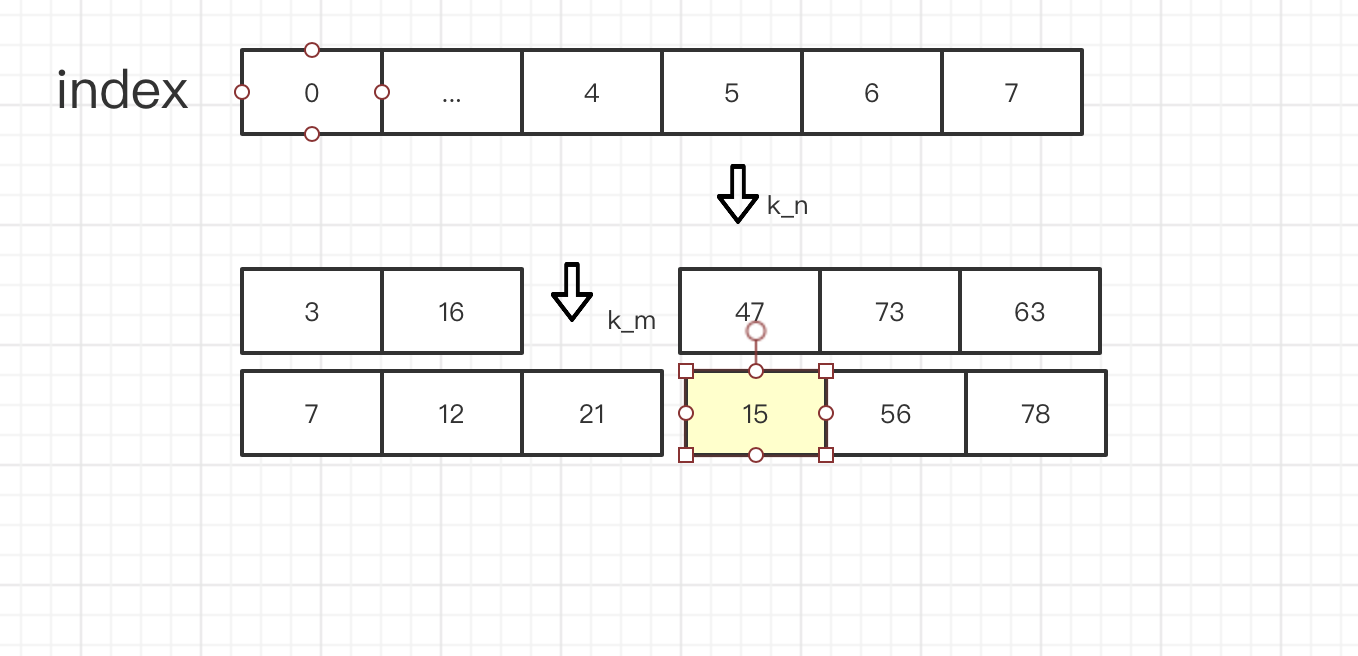
如果 k_m + 1 比 k_n小 故而插入到k_n前面 那么 k_m + 1 就一定 是紧挨着 47的吗?如果 k_m + 1 比前面的 某 1个数还小呢?
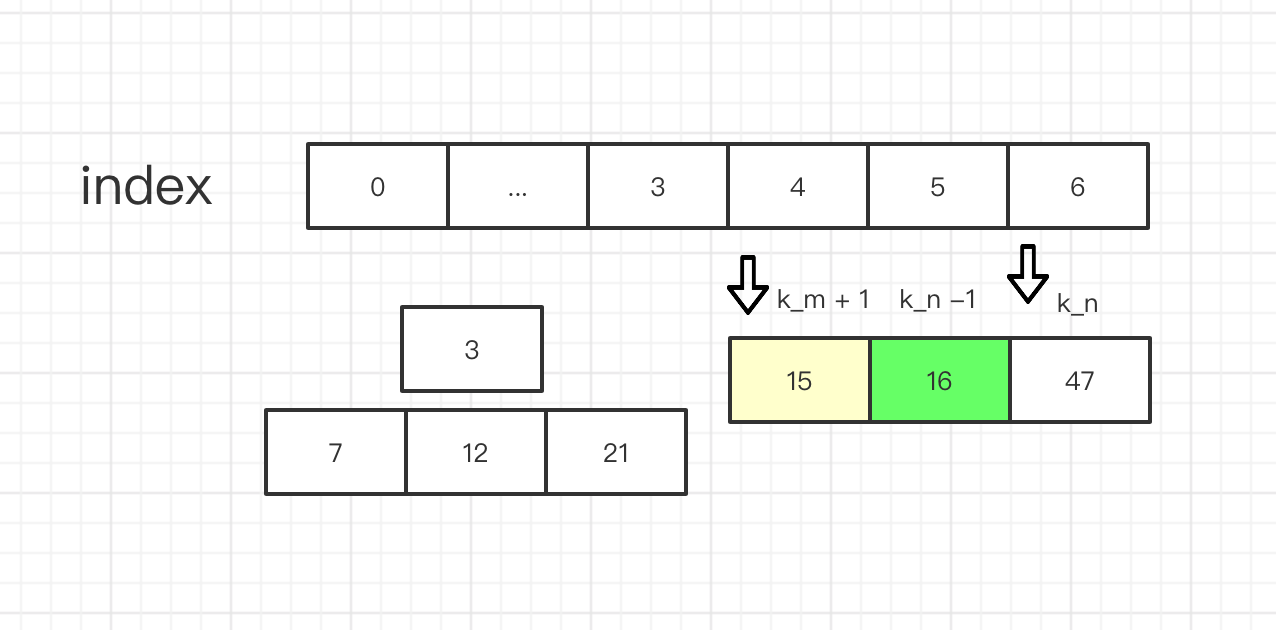
上图,我们可以看到 第 k_2 个数,因为另一组比它更小的数的插入,而导致 第k_2个数位置发生变化。
要想稳定得到 第k_2个数,那么 我们要 另一组数组的 第k_m + 1个数要大于等于 第 k_2个数,这也是最重要的条件
如果小于的话 我们就需要把 k_n 也就是 现在的 第 k_2 个数 往左移动一格,并且 把 k_m 往右移动 这样 就还是能维持 k_m + k_n = k_2。
例子
我们可以划分为,红线以左指针区域 和 红线的以右指针右边区域,
当我们 求 中位数
如果是 偶数 就是 (max{指针区域} + min{指针右边区域}) /2
如果是 奇数时 max{指针区域} 。
为什么呢 ,因为我们定义了 我们的2个指针中永远有一个 是指向第k_2个数,另一个指向k_2 -1,此时我们假设 k_2 是中位数,那么 k_2 -1 < k_,那么 求 max 就可以找到了。
如果是 奇数情况 我们只要找指针 直接求max 返回就可以。
如果是偶数的情况,那么 给定数组是有序的,假设 k_2 后面那个数 叫 k_2 + 1 那么 k_2 + 2 > k_2 + 1 > k_2,所以 min{ k_2 + 2 , k_2 + 1} 就可以得到 k_2 + 1了。
所以 偶数个 计算中位数就是 (max{指针区域} + min{指针右边区域}) /2
上面我们提到 我们定义了 2根指针指向了,k_m 和k_n 永远有一根是中位数。那么怎么找到 中位数呢?
我们只需要 保证 指针区域 的值 都小于 指针右边区域 其实就可以了.
如果不小于 我们就 一个往左移动指针,另一个往右移动指针,直到找到那么个区域,由于同时移动 一个 + 1 一个 减 1 那么 还是能保持 k_m + k_n = 2k.
但是我们 还要处理,边界的情况,
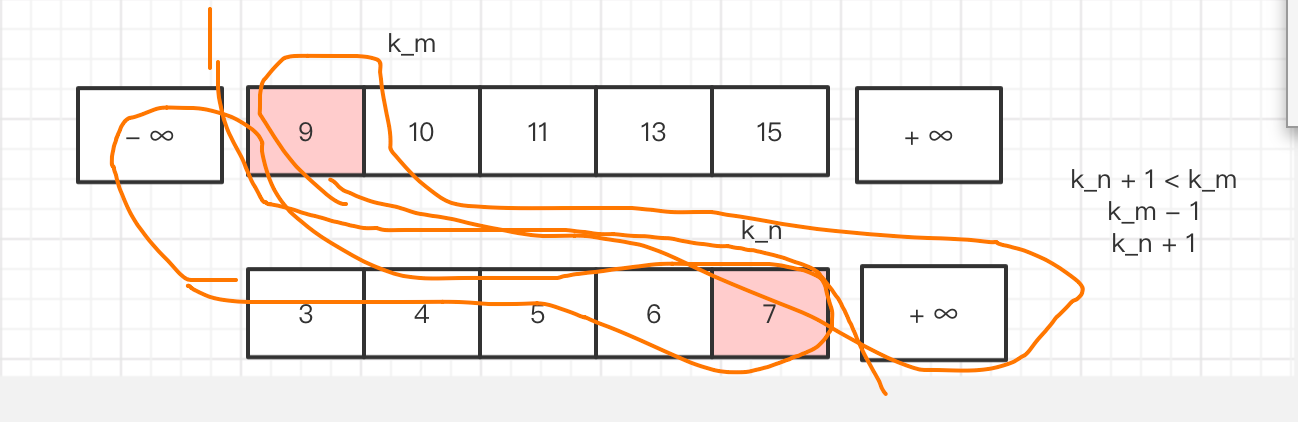
为了 处理 边界情况 我们 添加了 一些 不影响,中位数的数字 就是一些比较大的数字 和一些 比较小的数字
#![allow(unused_variables)] fn main() { std::i32::MIN std::i32::MAX }
然后 就算 是边界,如上图 (max{-∞,7} + min{∞,9}) / 2= (7 + 9) / 2 也可以很好的计算了是不是。
为什么 下面那个数组 没有-∞ 实际上 按照我们的思路,一般不会出现 到边界 这种情况,除非什么空数组啊 什么的,但我们 对一些 比较麻烦的情况直接 偷懒 特殊处理。
完整代码:
pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64{ //偷懒 处理 都是 1个的情况 let iseve = (nums1.len() + nums2.len()) % 2 == 0; let mut nums1 = nums1; let mut nums2 = nums2; if nums1.len() > nums2.len(){ let tmp = nums1; nums1 = nums2; nums2 = tmp; } // 偷懒 解决数组有长度 一个数组 没长度 if nums1.len() == 0 { if iseve { return (nums2[(nums2.len())/2 -1] as f64 + nums2[(nums2.len() + 1)/2 ] as f64 )/ 2.00; }else{ return nums2[(nums2.len() + 1)/2 -1] as f64 } } let k_2 = (nums1.len() + nums2.len() + 1) / 2 -1; //k 为小的数 let mut k_m = nums1.len() -1; let mut k_n = 0; let k = k_2 / 2 ; if nums1.len() + nums2.len() != 2 { if k_m < k{ k_n = k_2 - k_m -1; }else{ k_m = k; k_n = k_2 - k -1 ; } } //交换数组 if nums1[k_m] < nums2[k_n] { let tmp = nums1; nums1 = nums2; nums2 = tmp; let tmp = k_n; k_n = k_m; k_m = tmp; } //这里 push 几个值 是为了 处理边界的情况 nums1.insert(0,std::i32::MIN); nums2.push(std::i32::MAX); nums1.push(std::i32::MAX); k_m +=1; //以下是 核心代码 上面预处理 没什么技术含量 while k_n + 1 < nums2.len() -1 && nums1[k_m] > nums2[k_n + 1]{ if k_m == 0 { k_n +=1; }else{ k_m -= 1; k_n +=1; } } if iseve { return (max(nums1[k_m],nums2[k_n]) as f64 +min(nums1[k_m +1],nums2[k_n +1]) as f64 )/ 2.00; }else{ return max(nums1[k_m],nums2[k_n]) as f64; } -1.0 } fn main() { let m = vec! [1,2] ; let n = vec! [3,4] ; println!("{}",find_median_sorted_arrays(m,n)); }
