Leetcode 第120题 三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

例如，给定三角形：

[ [2], [3,4], [6,5,7], [4,1,8,3] ]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

解题思路

首先 题目说了自上而下,然后只能往相邻的元素走, 相邻 就是 索引 一样 或者 索引 + 1, 所以 它的next 就是它下一层 的 索引和当前一样 或者索引 +1。

理论上 要找到 最小的路径和,我们要对所有可能要找的路径 进行计算然后取最小的。

动态规划

这题可以用动态规划的思想,一上来如果没有方向的话,我们 可以找一个小的子问题去解决它,也许写着写着 就有灵感了。那么 我们先尝试着看看 怎么找下一个相邻节点。

pub fn minimum_total(triangle: Vec<Vec<i32>>) -> i32 {
    let floor =  triangle.len() -1;
		// triangle.len() -1 最后一层没有下一个节点 不需要找
    for i in 0..triangle.len() -1{
        for j  in  0..triangle[i].len(){
            if  j + 1 < triangle[i + 1].len() {
                print!(" | {} next {} {}",triangle[i][j],triangle[i + 1][j],triangle[i + 1][j +1]);
            }else{
                print!("{} next {} ",triangle[i][j],triangle[i + 1][j]);
            }

        }
        println!();
    }
    1

}

fn main() {
    let angle:Vec<Vec<i32>> = vec![ vec![2], vec![3,4], vec![6,5,7], vec![4,1,8,3]];
    minimum_total(angle);

}

我们找到了,每一个数的下一个相邻节点,除了最后一层 没有下一个相邻节点,有了 相邻节点 我们就可以计算 当前 节点 到相邻节点的和了,有了这个基础 我们 只需要 把 每一步 和上一步的 值 相加 就可以得出答案了。

我的思路是 定义一个lastsummary 用来记录 上一层的信息。

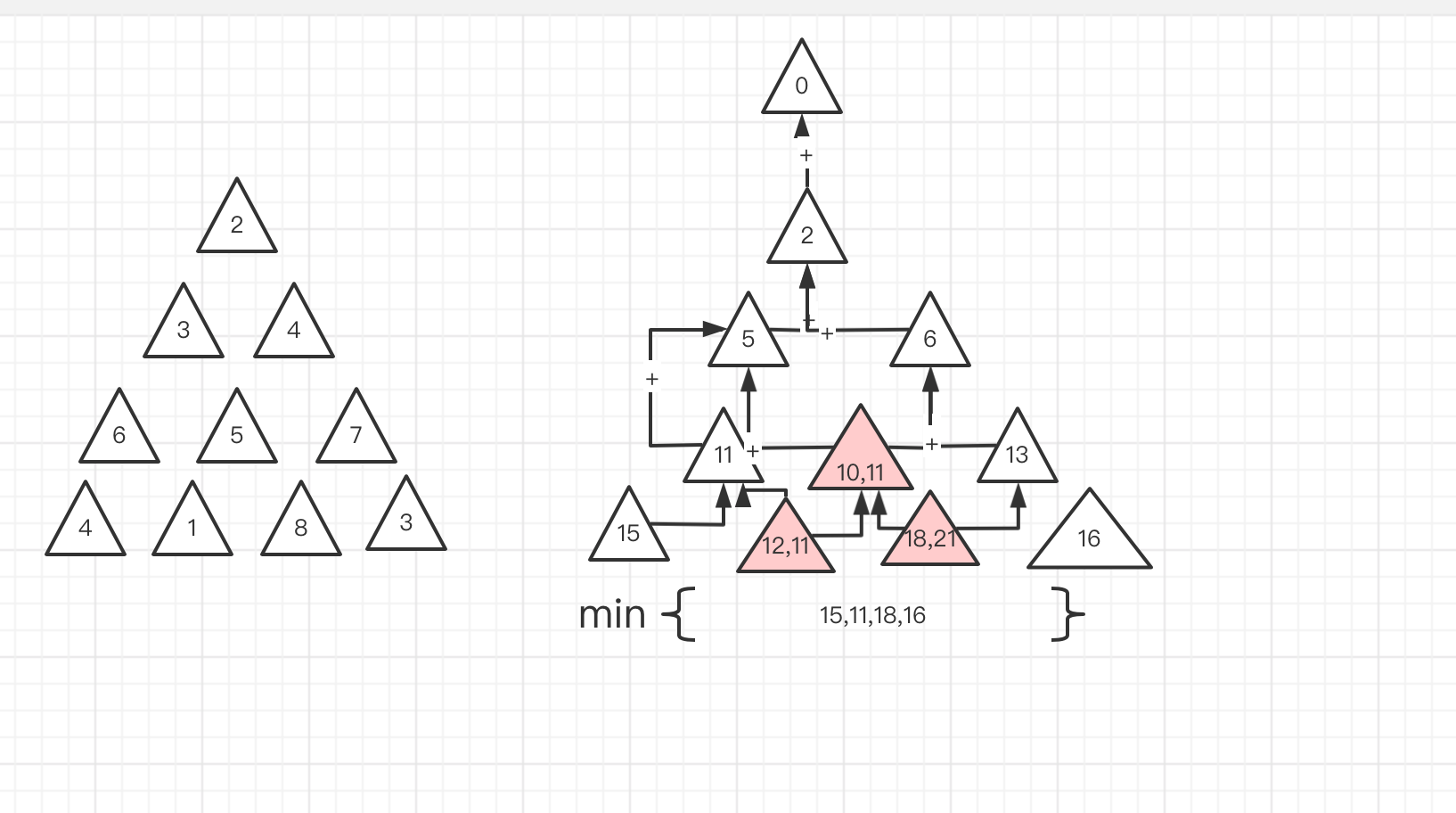
image-20200706200455342

如上图,每一个节点 是上一个节点之和, 由于只能往右,所以我们知道每一个节点的上一个节点 必然是 自身的index 或者 index-1 ,那么 我们一开始 使用一个 lastsummary 里面包含一个 0。

那么 第一层 2 + 0 =2 lastsummary =[2]

第二层 3 + 2 = 5 、4 + 2 = 6 lastsummary = [5,6]

我们是通过 当前index 和当前 index -1 索引 的 上一层的 lastsummary,如果 得出2个值,如第三层 10 和 11 ,它们其实所处的位置都是一样的 所以 2者我们取其中最小值,就可以了。

use std::cmp::{max, min};
pub fn minimum_total(triangle: Vec<Vec<i32>>) -> i32 {
    if  triangle.len() == 0{ return 0;}
    let  mut sum = vec![0];
    for i in 0..triangle.len(){
        let mut floor = vec![];
        for j  in  0..triangle[i].len(){
            if  j < 1 {
                floor.push(sum[j] + triangle[i][j]);
            }else if( j  == triangle[i].len() -1 ){
                floor.push(sum[j -1] + triangle[i][j]);
            } else {
                floor.push(min(sum[j-1] + triangle[i][j],sum[j] + triangle[i][j]));
            }
        }
        sum = floor;
    }
    *sum.iter().min().unwrap()
}
fn main() {

    let angle:Vec<Vec<i32>> = vec![ vec![-1], vec![2,3], vec![1,-1,-3]];
    println!("{}",minimum_total(angle));
}

算法复杂度：O(n)

空间复杂度：O(n)

image-20200706201103414