Leetcode 第150题 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。

有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

  • 整数除法只保留整数部分。
  • 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入: ["2", "1", "+", "3", "*"] 输出: 9 解释: 该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入: ["4", "13", "5", "/", "+"] 输出: 6 解释: 该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入: ["10", "6", "9", "3", "+", "-11", "", "/", "", "17", "+", "5", "+"] 输出: 22 解释: 该算式转化为常见的中缀算术表达式为： ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

  • 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
  • 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

解题思路

这道题目,看起来好像挺麻烦的,但实际上 只要充分了解 栈的特性就很简单了,波兰表达式 应该是编译原理 里面的知识,可以用来实现一些语法解析 然后用栈 模拟进行计算,可以用来实现脚本语言。

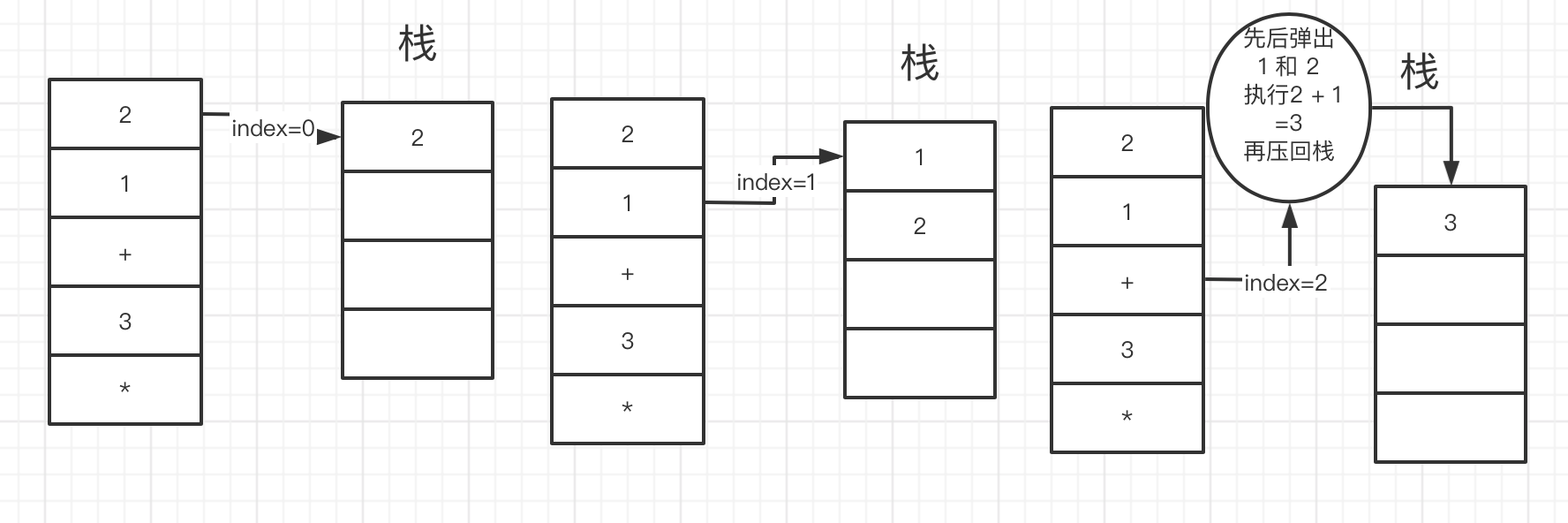
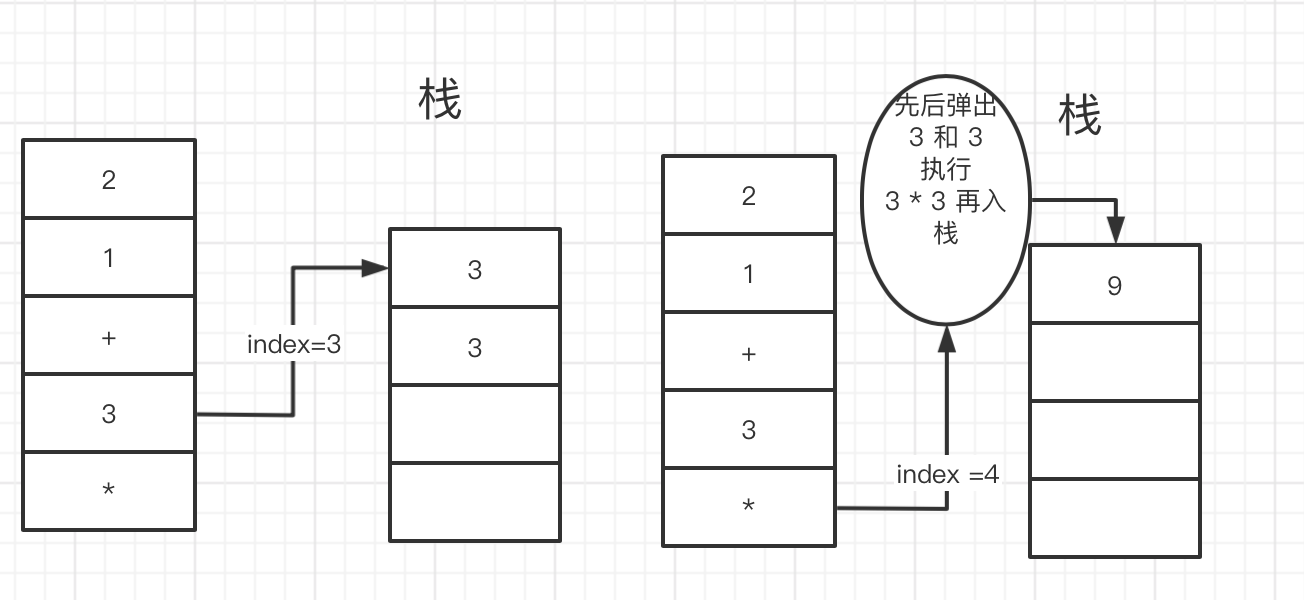
image-20200713193421530 image-20200713193438285

如上图 所以 我们要借助 一个数组当做栈 来处理数据。

#[macro_export]
macro_rules! pop {
    ($name:expr) => {
        $name.pop().unwrap()
    };
}
pub fn eval_rpn(tokens:Vec<String>) -> i32 {
    let mut stack:Vec<i32> = vec![];
    for i in 0..tokens.len(){
        let token = tokens[i].clone();
        match token {

            _ if token == "+" => {
                let first = pop!(stack);
                let second = pop!(stack);
                stack.push(second  + first);

            },
            _ if token == "-" => {
                let first = pop!(stack);
                let second = pop!(stack);
                stack.push(second - first);

            },
            _ if token == "*" => {
                let first = pop!(stack);
                let second = pop!(stack);

                stack.push(second * first);
            },
            _ if token == "/" => {
                let first = pop!(stack);
                let second = pop!(stack);
                stack.push(second/  first);
            },
            //如果是一个number 压栈
            _ => {
                stack.push(token.parse::<i32>().unwrap())
            }

        }
    }

   pop!(stack)

}

fn main() {
    let mut m:Vec<String> =Vec::new();
    m.push("2".parse().unwrap());
    m.push("1".parse().unwrap());
    m.push("+".parse().unwrap());
    m.push("3".parse().unwrap());
    m.push("*".parse().unwrap());
    let len = m.len()-1;
    println!("{:?}",m);
    let res = eval_rpn(m);
    println!("{}",res);
}

时间复杂度：O (n)

空间复杂度：O (n)

image-20200713192320769